Rückkopplung und Wachstumsprozesse
Wachstumsprozesse spielen nicht nur im biologischen Umfeld eine wichtige Rolle - beim "Wachstum" von Kristallen, bei der Anlagerung von Staubteilchen und zahlreichen Vorgängen, bei der Größen anwachsen oder abnehmen, können ähnliche Modelle zur Beschreibung eingesetzt werden.
Ein - auch im Zusammenhang mit der Teilchenbewegung - interessantes Modell bildet das Wachstumsmodell der zufälligen Anlagerung von Teilchen ("diffusionsbegrenztes Wachstum"). Die statistisch gleich verteilte Bewegung kleinster Teilchen führt durch Anlagerung zu bemerkenswert regelmäßigen Strukturen, die sich ähnlich wie Fraktale beschreiben lassen. Im Abschnitt "Teilchenbewegung" stehen eine Physlet-Animation, und im vorliegenden Abschnitt zum "Wachstum" zwei Modelle zur Auswahl, die die Anlagerung von Russteilchen oder diffusionsbegrenztes Wachstum zeigen.
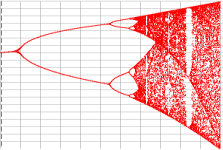Das Modell vom logistischen Wachstum öffnet eine interessante Querverbindung zu einem modernen Wissensgebiet der Physik, der Chaosforschung: Wie sich, unter bestimmten Voraussetzungen, eine Population entwickelt wird in der logistischen Gleichung an Hand eines Parameters beschrieben. Je nach seinem Wert ergeben sich einzelne oder mehrere Grenzwerte, oder die Population entwickelt sich unvorhersagbar... (vgl. Verhulst-Modell, Feigenbaum-Diagramm).