Lernpfad: Ort, Zeit und Bewegung
Fahre v - denke v2!
Geschwindigkeit
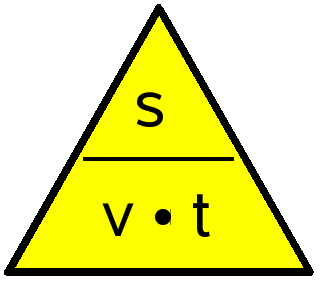Die Geschwindigkeit v beschreibt für die gleichförmige Bewegung, wie weit ein Körper in einer bestimmten Zeitspanne gekommen ist:
Δ s = v . Δ t (v ... Geschwindigkeit, Δ s ... die zurück gelegte Wegstrecke, Δ t ... die dazu benötigte Zeit)
Berechne für verschiedene Geschwindigkeiten v und verschiedene Zeitspannen Δ t, wie weit der Körper gekommen ist (Tipp):
Du siehst: Der zurückgelegte Weg ist bei gegebener Geschwindigkeit v der Zeit t proportional; und der zurückgelegte Weg ist bei gleichbleibender Zeit t der Geschwindigkeit v proportional...
Untersuche dies hier genauer ...
Eine anschauliche Darstellung der gleichförmigen Bewegung findest du hier.
Die Geschwindigkeit v ist der Quotient aus dem zurückgelegten Weg Δ s durch die dazu benötigte Zeit Δ t:
v = Δ s / Δ t
Die Einheit der Geschwindigkeit ist m/s.
Beschleunigung
Bleibt die Geschwindigkeit nicht gleich, so sagt man, eine Bewegung erfolgt beschleunigt. Die Beschleunigung a ist der Quotient aus der Geschwindigkeitsänderung Δ v durch die dazu benötigte Zeit Δ t:
a = Δ v / Δ t
Die Einheit der Beschleunigung ist m/s2.
Berechne einige Beschleunigungswerte, indem du abschätzt, in welcher Zeitspanne Δ t sich die Geschwindigkeit um Δ v verändert hat (Tipp):
- Wann sind Beschleunigungswerte positiv, wann negativ?
- Vergleiche deine Ergebnisse mit dem Wert für die "Fallbeschleunigung" g auf der Erde: g = 9.80665 m/s2
- Recherchiere verschiedene Beschleunigungswerte aus der Praxis und verwende diese Werte für Berechnungen auf dieser Seite!
Zeitgewinn durch erhöhte Geschwindigkeit?
Eines steht fest: Wenn du schneller fährst, dann legst du die gleiche Strecke in einer kürzeren Zeitspanne zurück. Die Frage ist nur: Wie viel Zeit gewinnst du, wenn du "rast"?
Untersuche dies hier genauer ...
Die Crux: der Anhalteweg!
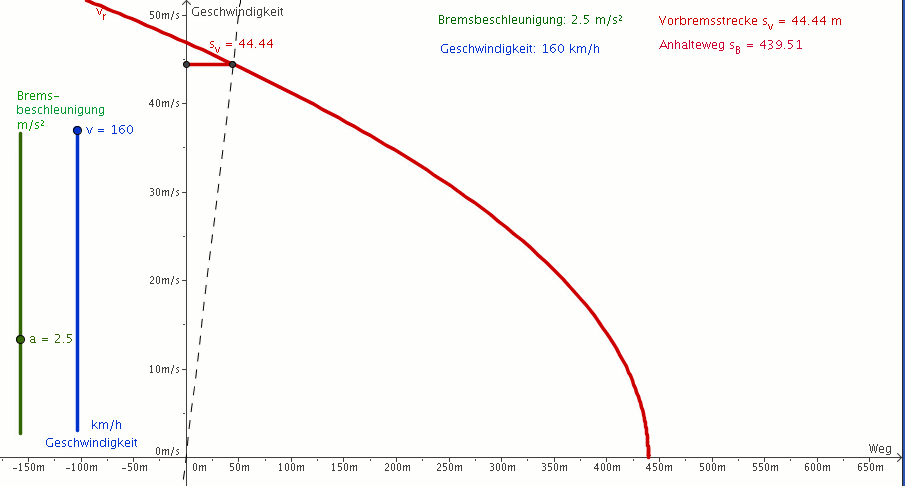
Der Anhalteweg setzt sich aus der Vorbremsstrecke und aus dem eigentlichen Bremsweg zusammen. Während der "Schrecksekunde" bewegt sich das Fahrzeug nahezu gleichförmig weiter; danach wird es bis zum Stillstand abgebremst (näherungsweise eine gleichmäßig beschleunigte Bewegung). Untersuche dies hier genauer!
Und wie geht es weiter?
An dieser Stelle haben wir nur Bewegungen untersucht, die gleichermäßen nur in eine Richtung (also beispielsweise "der Straße entlang") erfolgten. Tatsächlich spielen bei zahlreichen Beweung so genannte "Richtungsänderungen" eine entscheidende Rolle: Kurven fahren im Verkehr, viele Bewegungen im Sport, zusammengesetzte Bewegungen (zB Wurfbewegungen) etc.
Lies hier zur Rotation weiter.
Lies hier zum Schiefen Wurf nach!
GeoGebra - www.geogebra.at